datalab-handout

温馨提示：内有解法剧透，未完成前请不要阅读。其中代码，仅供本人回忆用。

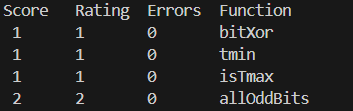
bitXor

要求我们使~和&这两个位运算符实现异或运算，最大操作次数不超过14次。

我们扩大条件，考虑~，&，|这三个位运算如何实现异或。比较容易想到 $(!a\&b)|(a\&!b)$ 即可实现异或运算。（这里的!指的是~)。

a = 0, b = 0, (!0\&0)|(0\&!0) = 0|0 = 0\\ a = 1, b = 0, (!1\&0)|(1\&!0) = 0|1 = 1\\ a = 1, b = 1, (!1\&1)|(1\&!1) = 0|0 = 0\\

考虑将|转化为&，则有

!(!((!a\&b)|(a\&!b))) = !((!(!a\&b))\&(!(a\&!b)))

然后我们使用代码实现即可。成功通过测试。我们共使用8次位运算解决。

1
2
3

int bitXor(int x, int y) {
  return ~((~((~x)&y))&(~(x&(~y))));
}

tmin

可用运算符：! ~ & ^ | + << >>

最大运算次数：4

要求我们使用上述运算符求得最小整数的补码。(1<<31)即可，当符号位为1，且其余位为0时即表示整数的最小值。由于0的原因，负数的表示范围比整数多1。

1
2
3

int tmin(void) {
  return (1 << 31);
}

isTmax

Legal ops: ! ~ & ^ | +

Max ops: 10

判断一个数是否是int能表示的最大值，如果是返回1，否则返回0。容易注意到当x为最大值时，加1会发生溢出成最小值，所以x+x+1=-1。当x=-1时，也会使x+x+1=-1，所以我们需要对x=-1时特判，当两个条件都符合时，这个数即为最大值。

int isTmax(int x) {
//  return  !((((1 << 31) + ((~1) + 1)))^x); //2024/4/13 20:22 update: 没有注意到不能使用<<，已更新。
    return (!((x+(x+1))^(~0)))&!!(x^~0);
}

allOddBits

Legal ops: ! ~ & ^ | + << >>

Max ops: 12

设计一个函数，检查一个整数所有奇数位是否全部为1。例如，1010，return 1。显然我们可以先构造一个奇数位全1的数tmp，然后将tmp&x如果结果为tmp，那么代表x符合要求，最后将(tmp&x)^tmp取！即可。共3次操作。

int allOddBits(int x) {
  //int tmp = 0xAAAAAAAA;    2024/4/13 20:22 update: 没有注意到只能使用0x00-0xff直接的常量
  int tmp = 0xAA + (0xAA << 8) + (0xAA << 16) + (0xAA << 24);
  return !((tmp&x)^tmp);
}

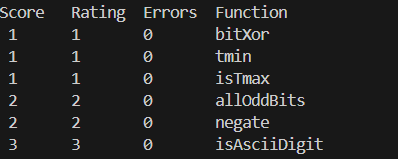
negate

Legal ops: ! ~ & ^ | + << >>

Max ops: 5

返回x的补码，对x取反后+1即可。不是特别理解这个题出现在前面四题的后面，而且分值比前面的题高。实际上在前面的题目实现中我就已经实现了该功能。

1
2
3

int negate(int x) {
  return (~x) + 1;
}

isAsciiDigit

Legal ops: ! ~ & ^ | + << >>

Max ops: 15

判断输入的整数是否在’0’到’9’之间。思路，判断x-‘0’与’9’-x是否都>=0即可，我们可以通过符号位来进行判断，如果&上(1<<31)不为0，则代表该数<0，再结合之前的负数表示，可以很轻松的解出本题。共14次操作，稍微有点极限。

int isAsciiDigit(int x) {
  int l = ((x + (~0x30) + 1) & (1 << 31));
  int r = ((0x39 + (~x) + 1) & (1 << 31));
  return (!l&!r);
}

conditional

Legal ops: ! ~ & ^ | + << >>=

Max ops: 16

本题实现类似x?y:z的三元操作符，如果x非0，则返回y，否则返回z。我们可以考虑一个思路，让y&flag，z&~flag，并且返回他们的或，当x非0时，flag为全1，~flag为全0，否则反之。flag如何构建呢？!x-1即可，当x为0时，flag=!x-1 = 0，~flag为全1，反之，flag=!x-1=-1，由于是补码表示，所以-1就是全1。总共8次操作即可完成。

int conditional(int x, int y, int z) {
  int f = !x + ~1 + 1;
  return (f&y)|((~f)&z);
}

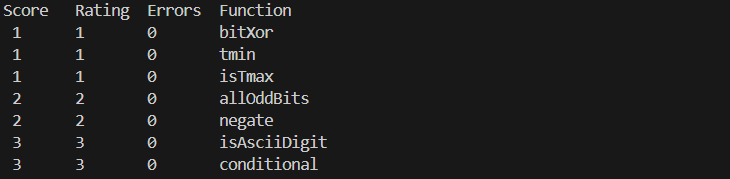
isLessOrEqual

Legal ops: ! ~ & ^ | + << >>

Max ops: 24

if x <= y then return 1, else return 0

延续上面的思路，用x-y，然后判断符号位即可，-y可以用补码代替。但是会有一个问题，当x为最大值，y为最小值时会发生溢出，导致我们判断错误。所以我们首先要判断x和y是否同号，如果不同号则直接比较符号位，同号时再判断x-y的符号位，这样就保证了不会出现溢出。共使用了22次操作，略微极限。

1
2
3

int isLessOrEqual(int x, int y) { 
  return ((!((y + ~x + 1) & (1 << 31)) & !((x&(1<<31))^(y&(1<<31)))) | (!(!(x&(1<<31)))&(!(y&(1<<31)))));
}

logicalNeg

Legal ops: ~ & ^ | + << >>

Max ops: 12

implement the ! operator

我们需要实现！运算符，当x不为0时，返回0，否则返回1。因此我们需要找到0的独特性质，0的符号位为0，0-1的符号位为1，所以如果x>>31后与1为0，且(x-1)>>31后与1为1，那么返回0，否则返回1。共9次操作。

1
2
3

int logicalNeg(int x) {
  return (((x+~1+1)>>31)&1)&~((x>>31)&1);
}

howManyBits

Legal ops: ! ~ & ^ | + << >>

Max ops: 90

x被能最少多少位的补码所表示。——这个题比较难，暂时没什么思路。等把课程看完再补后续(2024/4/12)。

对于正数01001，则可以用4+1位表示，也就是数值位+1。对于负数11001，我们可以对其取反后00110，用3位+1位表示，实际上11001等价1001，也就是4位。（它们都表示-7）。所以我们可以通过x>>y位后是否为0来判断它所需位数是否大于y。因为我们最多用31位数值位表示，所以我们可以用二进制构造1111111来进行判断，首先判断16，如果>0，则将原数右移16，再依次判断，否则直接往下判断。(2024/4/14)。

int howManyBits(int x) {
  int s = (x >> 31);
  int a  = ((s&(~x)) + (~s&(x)));
  int b16 = (!!(a>>16))<<4;
  int b8,b4,b2,b1;
  a=a>>b16;
  b8 = (!!(a>>8))<<3;
  a=a>>b8;
  b4 = (!!(a>>4))<<2;
  a=a>>b4;
  b2 = (!!(a>>2))<<1;
  a=a>>b2;
  b1 = (!!(a>>1))<<0;
  a=a>>b1;
  return b16 + b8 + b4 + b2 + b1 + 1 + a;
}

floatScale2

Max ops: 30

传入一个无符号整数表示浮点数x，将x*2的结果返回。分三种情况：

exp = 0，则直接将尾数左移一位即可。
exp = 11111111，则直接返回x，因为代表无穷大或者NaN。
其他情况则将exp+1，然后把结果组装返回。

unsigned floatScale2(unsigned uf) {
  int s = uf&(1<<31);
  int exp=((uf)&(0xff<<23));
  int frac = (uf&0x7fffff);
  if(exp == (0xff)<<23) return uf;
  if(exp!=0) exp+=(1<<23);
  else frac<<=1;
  return (s^0)+exp+frac;
}

floatFloat2Int

Max ops: 30

将浮点数的二进制表示转化为整数，如果超过表示范围就返回0x80000000u。我们将尾数取出并且补全到30位，并且将30位置为1。然后我们根据exp的取值范围进行不同的操作。

如果exp>30，则直接返回0x80000000u。一个int只能表示31位的整数，因为尾数隐藏了一个1，所以如果exp=31，这将是一个32位的整数，故超出了表示范围。
如果exp<0，则表明该浮点数小于1，直接返回0即可。

int floatFloat2Int(unsigned uf) {
  int s = (uf>>31)&1;
  if(s) s = -1;
  else s = 1;
  int exp=((uf>>23)&0xff)-127;
  int frac = (uf&0x7fffff) << 8;
  if(exp > 30) return 0x80000000u;
  if(exp < 0) return 0;
  return s * ((frac>>(30-exp))+(1<<exp));
}

floatPower2

Max ops: 30

返回2的x次幂，我们只需要构造出2的浮点表示，然后将exp+x即可，当然我们需要判断特殊情况，如果exp+x<0，则直接返回0；同时题目要求too large，返回INF，也就是exp为0xff，尾数为0的浮点数。

unsigned floatPower2(int x) {
    unsigned uf = 0x3f800000;
    int exp = 0x7f + x;
    if(x < -0x7f) exp = 0;
    if(exp > 0xff) exp = 0xff;
    uf = (0<<31) + (exp<<23);
    return uf;
}

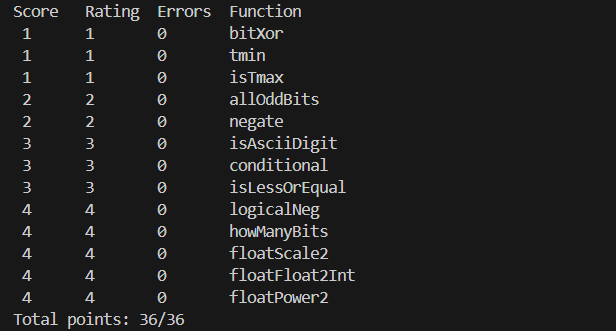
(2024/4/14)通关。