Floating Point

Floating Point Representation

Normalized Values

Numerical Form:

(-1)^s*M*2^E

S is a sign bit, it determines whether number is negative or positive.
Significand M normally a fractional value in range [1.0,2.0).
E weigths value by power of 2.

Single precision: 32 bits
s:1	exp:8-bits	frac:23-bits
Double precision: 64 bits
s:1 exp:11-bits frac:52-bits

E = Exp - Bias

Exp: unsigned value of exp field.
Bias = $2^{k-1}-1$ $2^{k - 1} - 1$ , k is number of exp’s bits
- Single precision: $2^7-1=127$
- Double precision: $2^{10}-1$ =1023

M= $1.xxxxxxx_2$ ，there first 1 is not stored.

Example

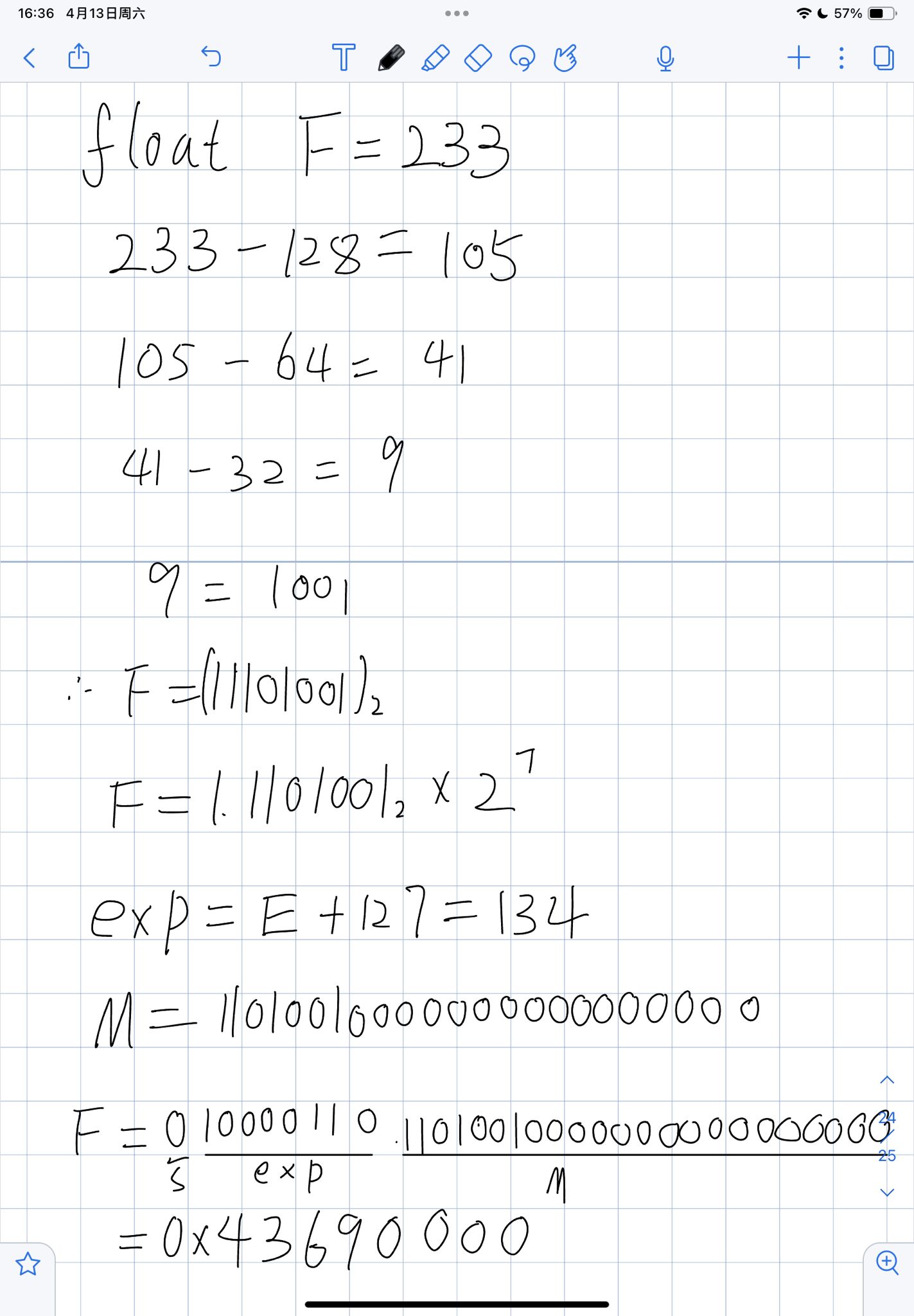
Denormalized Values

Condition:exp=000…0

E=1-Bias(instead of E = 0-Bias)

Significand coded with implied leading 0: M = $0.xxxxxx_2$

it’s usually represents closest to 0.0

exp = 0, frac = 0, Represents zero value.

Special Values

Condition:exp=111…1

Case:exp=111…1, frac = 0, infinity,E.g.1.0/0.0=-1.0/-0.0=positive infinity，1.0/-0.0=negative infinity

Case:exp=111…1,frac!=0, NaN

Round-To-Even

When exactly halfway between two possible values,Round so that least significant digit is even

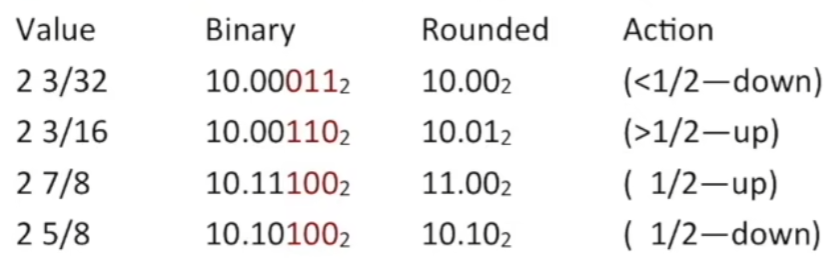
Multiplication

(-1)^{s_1}*M_1*2^{E_1}*(-1)^{s_2}*M_2*2^{E_2}

Exact Result: $(-1)^s*M*2^E$

Sign s : $s_1$ ^ $s_2$
Significand M : $M_1*M_2$
Exponent E : $E_1+E_2$

if M>=2，shift M right, increment E

if E out of range, oveflow

Round M to fit frac precision

Addition

(-1)^{s_1}*M_1*2^{E_1}+(-1)^{s_2}*M_2*2^{E_2},E_1>E_2

Exact Result: $(-1)^sM2^{E}$

E : $E_1$
M : line up the binary points and add $M_1,M_2$

float point addition is not commutative compliance law

1	(3.14+1e10)-1e10=0, 3.14+(1e10-1e10)=3.14

（update date：2024/4/13）

Machine-Level Programming I: Basics

Assembly/Machine Code View

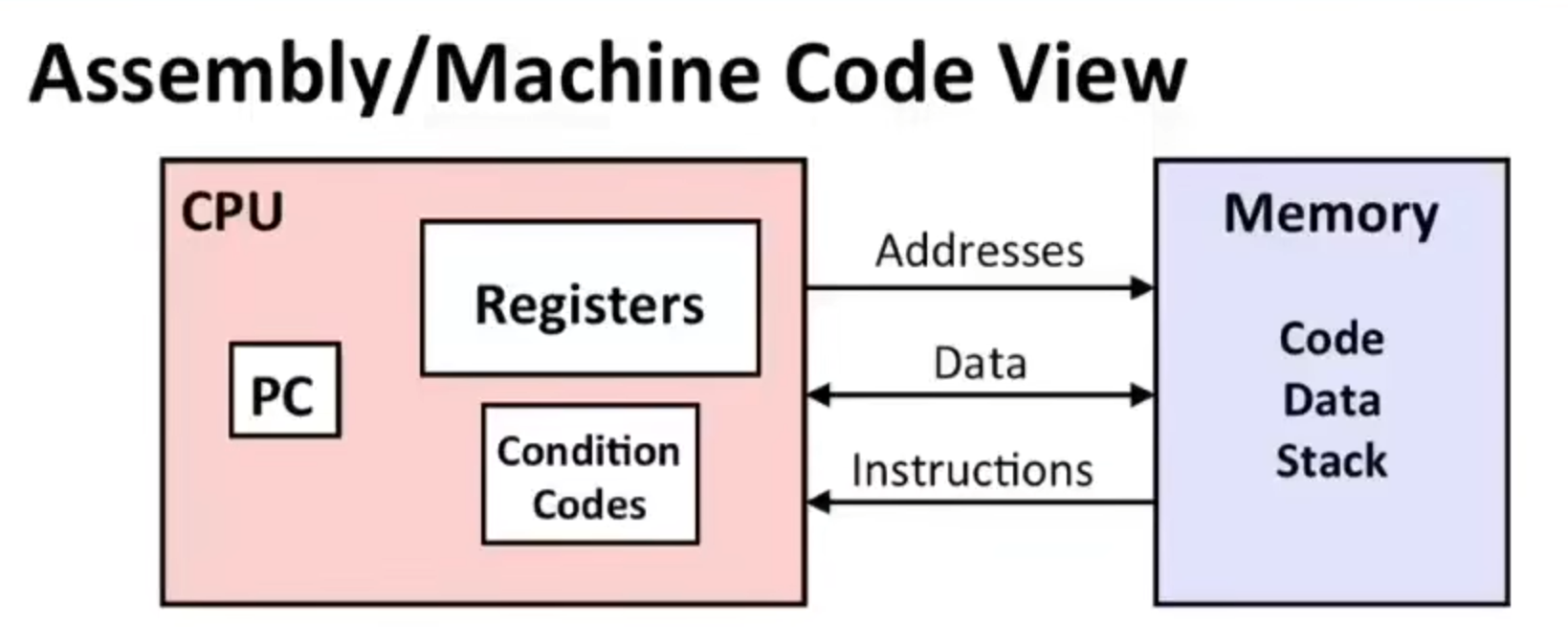
PC:Program counter

Address of next instruction
Called “RIP”(x86-64)

Heavily used program data

Condition codes

Store status information about most recent arithmetic or logical operation
used for conditional branching

Memory

Byte addressable array
Code and user data
Stack to support procedures

Assembly Characteristics

DataType

integer data of 1, 2, 4, 8bytes

Data values
Addresses(untyped pointers)

Floating point data of 4, 8, or 10 bytes

Code:Byte sequences encoding series of instructions

Arrays or structures: just contiguously allocated bytes in memory

Operations

Example

C : store value t where designated by dest

1	*dest = t;

Assembly : Move 8 byte to memory.

moveq %rax, (%rbx)
t:Register %rax
dest:Register %rbx
*dest:Memory M[%rbx]

Object Code: 3-byte instruction stored at address 0x40059e

1	0x40059e: 48 89 03

Disassembly

We can use gdb to get assembly.

1	gdb ./bomb

also, We can get same bytes on a address.like this, I can get string by address.(/s is ask to gdb use which way to get bytes)

X86-64 Interger Registers

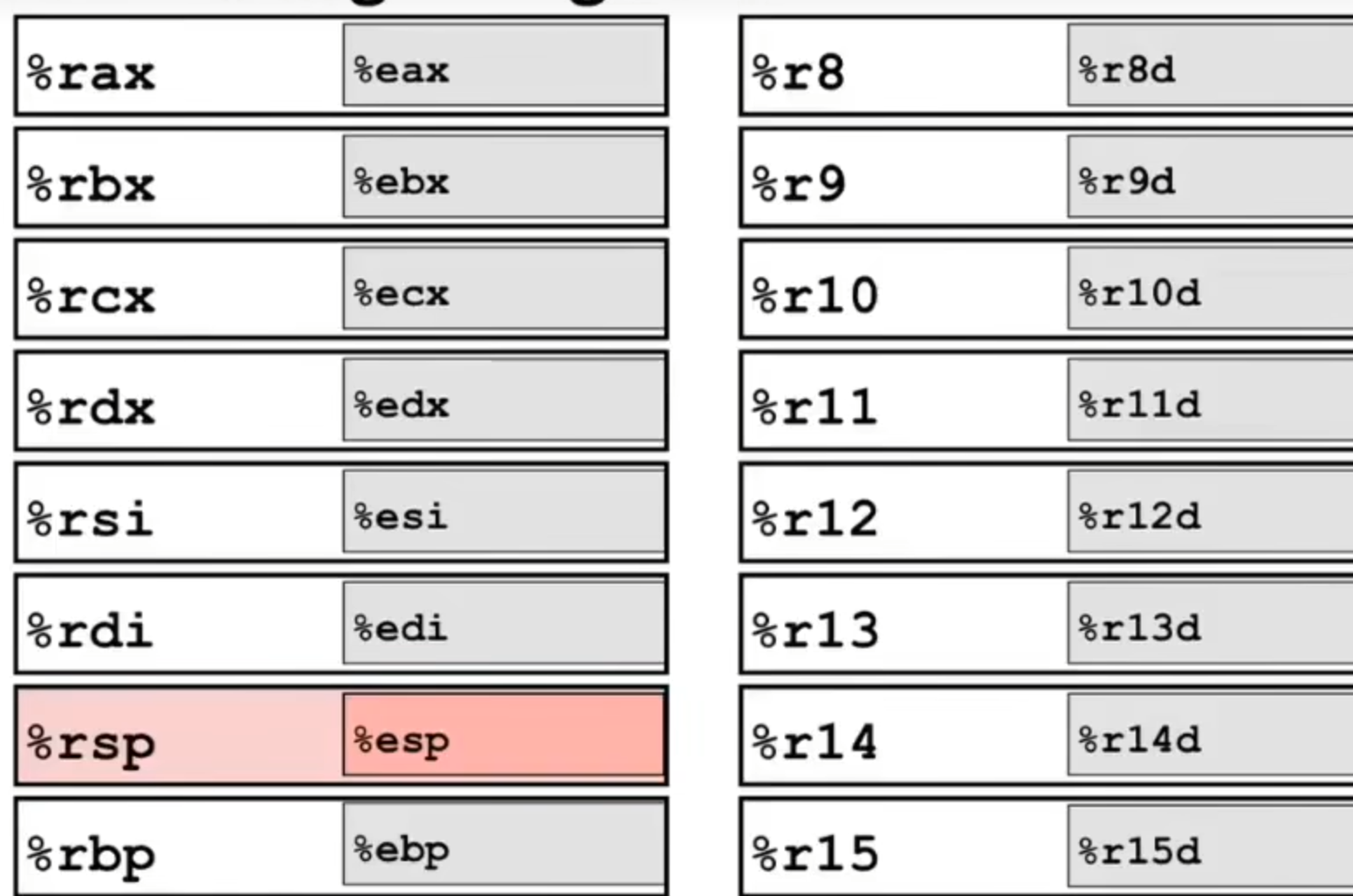
Can reference low-order 4 bytes (also low-order 1 & 2 bytes)

Moving Data

movq Source, Dest;

Cannot do memory-memory transfer with a single instruction.

example

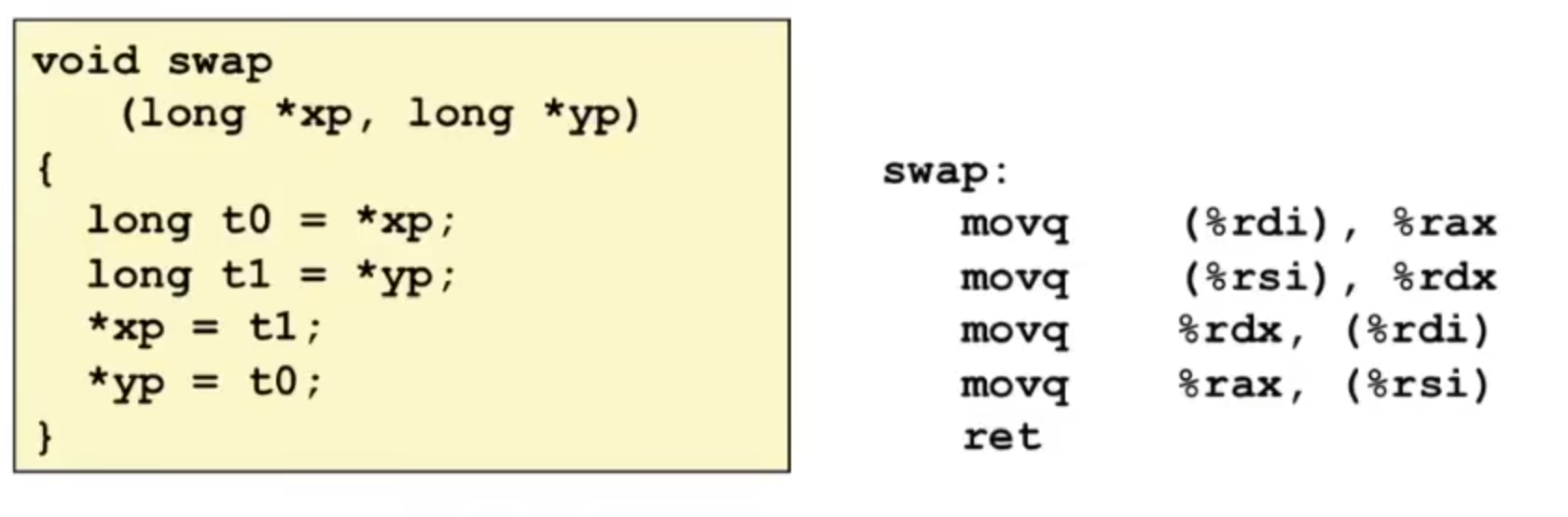
Most General Form

D(Rb,Ri,S) Mem[Reg[Rb]+S*Reg[Ri]+D]

D: Constant “displacement” 1, 2 or 4 bytes

Rb: Base register: Any of 16 integer registers

Ri: index register: Any, except for %rsp

S: Scale: 1,2,4, or 8

Address Computation Instruction

leaq Src, Dst

Src is address mode expression
Set Dst to address denoted by expression

long m12(long x) {
	return x * 12;
}
leaq (%rdi, %rdi, 2), %rax // rax = rdi + 2*rdi = 3*rdi
salq $2, %rax // rax = rax<<2 = rax*4 = 12*rdi

Some Arithmetic Operations

(update date: 2024/4/14)