CSAPP-note-4

Arrays

Array Allocation

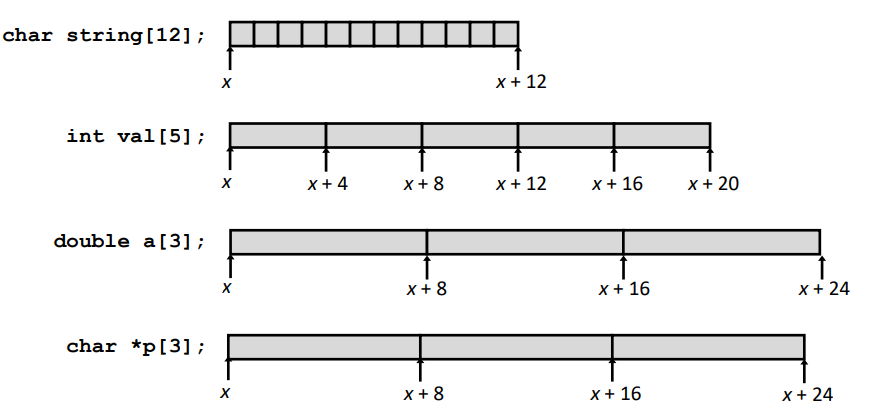
Basic Principle：T A[L];

• Array of data type T and length L
• Contiguously allocated region of L*sizeof(T) bytes in memory

Array Access

int val[5] = {1, 5, 2, 1, 3};

表达式	类型	值或含义
val[4]	int	3
val	int *	x
val+1	int *	x+4
&val[2]	int *	x+8
val[5]	int	??
*(val+1)	int	5
val + i	int *	x+4*i

Example

#define ZLEN 5
typedef int zip_dig[ZLEN];
zip_dig cmu = {1,5,2,1,3};
zip_dig mit = {0,2,1,3,9};
zip_dig ucb = {9,4,7,2,0};

Array Accessing Example

int get_digit(zip_dig z, int digit) {
    return z[digit];
}

传入zip，获取zip的第digit位，对应的汇编代码为

get_digit:
.LFB23:
        .cfi_startproc
        endbr64
        movslq        %esi, %rsi
        movl        (%rdi,%rsi,4), %eax
        ret
        .cfi_endproc

%rdi是数组的首地址，%rsi是数组的下标。int的大小为4个字节，所以第%rsi个元素对应的内存地址为%rdi+4*%rsi.

Array Loop Example

void zincr(zip_dig z) {
    size_t i;
    for (i = 0; i < ZLEN; i ++) {
        z[i]++;
    }
}

遍历数组每一个元素，并使其加一。

        movl        $0, %eax # i = 0
        jmp        .L2       # goto middle
.L3:                         # loop:
        leaq        (%rdi,%rax,4), %rcx # %rcx = %rdi + 4*%rax = z + i
        movl        (%rcx), %esi  # %esi = z[i]
        leal        1(%rsi), %edx # %edx = z[i] + 1
        movl        %edx, (%rcx)  # z[i] = % edx
        addq        $1, %rax      # i ++
.L2:
        cmpq        $4, %rax    # if i <= 4
        jbe        .L3
        ret

Multidimensional Arrays

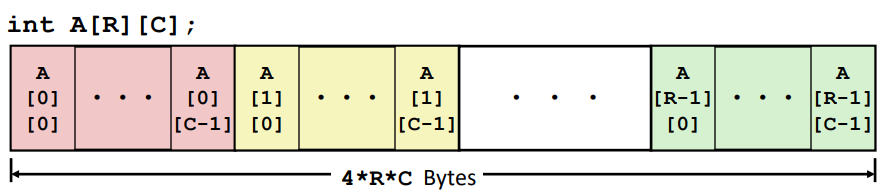
Declaration T A[R][C];

• 2D array of data type T
• R rows, C columns

Array Size RCsizeof(T) bytes

example

#define PCOUNT 4
typedef int zip_dig[5];

zip_dig pgh[PCOUNT] = {
    {1,5,2,0,6},
    {1,5,2,1,3},
    {1,5,2,1,7},
    {1,5,2,2,1}
};

zip_dig pgh[4]等价于int pgh[4][5]。

Nested Array Row Access

A[i] is array of C elements of type T.Starting address A + i * (C * sizeof(T))

get_pgh_zip:
.LFB23:
        .cfi_startproc
        endbr64
        movslq        %edi, %rdi
        leaq        (%rdi,%rdi,4), %rdx # 5 * index
        leaq        pgh(%rip), %rax     # 取出pgh的地址
        leaq        (%rax,%rdx,4), %rax # pgh + 20 * index
        ret

A[i][j] is element of type T, which requires K bytes

Address A + i * (C * K) + j * K = A + (i*C + j) * K

get_pgh_digit:
   0x0000000000001129 <+0>:     endbr64 
   0x000000000000112d <+4>:     movslq %esi,%rsi
   0x0000000000001130 <+7>:     movslq %edi,%rdi
   0x0000000000001133 <+10>:    lea    (%rdi,%rdi,4),%rax # 5*index
   0x0000000000001137 <+14>:    add    %rsi,%rax          # 5*index + dig
   0x000000000000113a <+17>:    lea    0x2edf(%rip),%rdx        # 0x4020 <pgh>
   0x0000000000001141 <+24>:    mov    (%rdx,%rax,4),%eax # M[pgh + 4*(5*index + dig)]
   0x0000000000001144 <+27>:    ret    

Array Elements

• pgh[index][dig] is int
• Address: pgh + 20index + 4dig = pgh + 4*(5*index + dig)

Multi-Level Array example

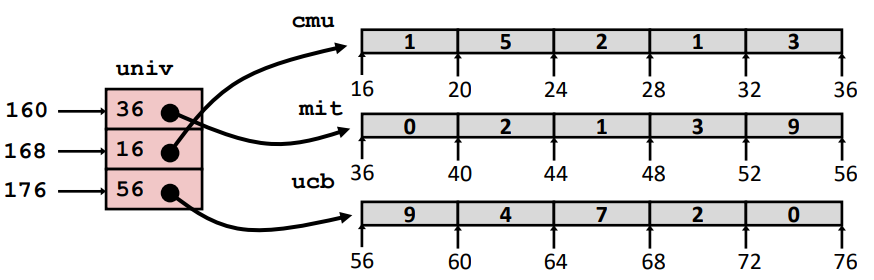
#define UCOUNT 3
typedef int zip_dig[5];

zip_dig cmu = {1,5,2,1,3};
zip_dig mit = {0,2,1,3,9};
zip_dig ucb = {9,4,7,2,0};

int *univ[UCOUNT] = {mit, cmu, ucb};

Variable univ denotes array of 3 elements.Each element is a pointer 8 bytes.Each pointer points to array of int’s.

get_univ_digit:
   0x0000000000001129 <+0>:     endbr64 
   0x000000000000112d <+4>:     lea    0x2f3c(%rip),%rax        # 0x4070 <univ>
   0x0000000000001134 <+11>:    mov    (%rax,%rdi,8),%rax       # p = univ[index]
   0x0000000000001138 <+15>:    mov    (%rax,%rsi,4),%eax       # return *(p + 4*digit)
   0x000000000000113b <+18>:    ret 

Computation

• Element access Mem[Mem[univ+8index]+4digit]
• Must do two memory reads
  • First get pointer to row array
  • Then access element within array

NxN Matrix Code

Fixed dimensions.Know value of N at compile time.

#define N 16
typedef int fix_matrix[N][N];
int fix_ele(fix_matrix A, size_t i, size_t j) {
    return A[i][j];
}
Dump of assembler code for function fix_ele:
   0x0000000000001129 <+0>:     endbr64 
   0x000000000000112d <+4>:     shl    $0x6,%rsi    # 64 * i
   0x0000000000001131 <+8>:     add    %rsi,%rdi    # 64*i + A
   0x0000000000001134 <+11>:    mov    (%rdi,%rdx,4),%eax # Mem[A + 64*i + 4*j]
   0x0000000000001137 <+14>:    ret 

Variable dimensions, explicit indexing.

Traditional way to implement dynamic arrays

#define IDX(n, i, j) ((i)*(n)+(j))

int vec_ele(size_t n, int *A, size_t i, size_t j) {
    return A[IDX(n, i, j)];
}

Variable dimensions, implicit indexing.Now supported by gcc.

int var_ele(size_t n, int A[n][n], size_t i, size_t j) {
    return A[i][j];
}
var_ele:
   0x0000000000001129 <+0>:     endbr64 
   0x000000000000112d <+4>:     imul   %rdx,%rdi            # n*i
   0x0000000000001131 <+8>:     lea    (%rsi,%rdi,4),%rax   # A + 4*n*i
   0x0000000000001135 <+12>:    mov    (%rax,%rcx,4),%eax   # Mem[A + 4*n*i + 4*j]
   0x0000000000001138 <+15>:    ret 

Structures

结构体的声明

struct rec {
    int a[4];
    size_t i;
    struct rec *next;
}

结构体可以被看作是一个能足够装下内部所有成员的内存块。

结构体内部成员在内存中的存储顺序和声明顺序一致，即使有另外一个顺序可以让结构体的布局更紧凑。

编译器确定了结构体的整体大小和字段的位置，机器级程序对源代码中的结构体没有任何理解。

Linked List Loop

Example 1

long length(struct rec*r) {
    long len = 0L;
    while(r) {
        len ++;
        r = r->next;
    }
    return len;
}

上面是计算一个链表长度的C程序，下面是其对应的汇编代码。注意到每次从结构体取出下一个结点的指针时，我们访问的是结构体首地址+24处的内存。原因是？内存对齐，我们会在稍后对其进行详细探讨。

.L3:
        addq        $1, %rax # len ++
        movq        24(%rdi), %rdi # r = Mem[r+24]
        testq        %rdi, %rdi # Test r
        jne        .L3    # if !=0, goto L3
        ret

Example 2

让我们再来看一个链表赋值的例子，以加深对结构体成员访问的理解。

void set_val(struct rec*r, int val) {
    while(r) {
        size_t i = r->i;
        r->a[i] = val;
        r = r->next;
    }
}

这两个例子我们能看出，读取结构体内部成员的内存，就是使用结构体首地址+字段偏移。

.L3:
        movq        16(%rdi), %rax # i = Mem[r+16]
        movl        %esi, (%rdi,%rax,4) # Mem[r+4*i] = val
        movq        24(%rdi), %rdi # r = Mem[r+24]
        testq        %rdi, %rdi # Test r
        jne        .L3    # if !=0 goto loop
        ret

内存对齐

struct S1 {
    char c;
    int i[2];
    double v;
} *p;

猜测一下上面这个结构体的size？C语言初学者可能会以为是1+8+8=17。实际上，sizeof(struct S1)的值是24。为什么会这样？大小为B个字节的原始数据类型的首地址必须是B的整数倍。

在这个例子里，char为1字节，而int是4字节，所以char后面有3个字节填充。同样地，double为8字节，而前面是4+4+4=12，所以还需要填充4字节。总共有24字节。

对齐原则

• 对齐数据
  • 原始数据类型需要B字节
  • 地址必须是B的倍数
  • 在某些机器上是必需的；在x86-64上是推荐的
• 为什么要内存对齐？
  • 现代计算机架构的硬件被设计成以固定大小的块来访问内存，通常是4字节或8字节（取决于系统）。这意味着读取或写入没有对其到这些边界的数据可能导致多次内存访问，从而减慢性能。
  • 内存换成被组织成缓存行，通常长64字节。访问跨越缓存行的数据会导致效率低下，因为可能加载或存储多个缓存行。为了避免跨越缓存行边界，建议将数据至少对齐到16字节边界。这有助于最小化需要访问的缓存行数量，从而提高整体的内存访问效率。
  • 虚拟内存系统使用页面来管理内存分配，如果一块数据跨越了两个虚拟内存页面，访问它可能触发多次内存访问，由于额外的页面查找而减慢性能。

常见的对齐情况（x86-64)

1 byte: char, … 没有要求

2 bytes: short, …地址的最低位必须是0

4 bytes: int float, … 地址的低两位是0

8 bytes: double, long, char *, … 地址的低三位是0

结构体对齐规则

在结构体内部：必须满足每个元素的对齐要求

结构体整体：每个结构体都要对齐结构体内部元素的最大的对齐值K。初始地址和结构体长度必须是K的倍数。

节省空间

方法：定义结构体时，把大的数据类型放在前面。

struct S1 {
    char c;
    int i;
    char d;
};

// size : 12 = 1 + 3 + 4 + 1 + 3

struct S2 {
    int i;
    char c;
    char d;
}

// size : 8 = 4 + 1 + 1 + 2;