这一章主要介绍文法，并且快速游览一下下图所示的编译器前端模型。

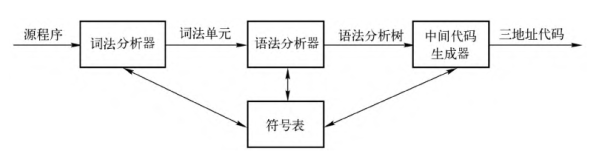
上下文无关文法

用于描述程序设计语言语法的表示方法——“上下文无关文法“，简称“文法”。文法被用于组织编译器前端。

产生式

文法自然地描述了大多数程序设计语言构造的层次化语法结构。例如，java中的if-else语句通常有如下形式

1	if(expression) statement else statement

我们用变量expr表示表达式，用变量stmt表示语句，那么这个构造规则可以表示为

1	stmt -> if(expr) stmt else stmt

其中->，可以读作“可以具有如下形式”。这样的规则称为产生式(production)。在一个产生式中，像if和括号这样的词法元素称为终结符号（可以简单理解成token，组成语句的基本单位）。像expr和stmt这样的变量表示终结符号的序列，它们称为非终结符号（nonterminal）（可以简单认为多个token组成的语句/表达式）。

文法定义

一个上下文无关文法由四个元素组成：

一个终结符号集合，也称为“词法单元”。终结符号是该文法所定义的语言的基本符号的集合。
一个非终结符号集合，也称为“语法变量”。每个非终结符号表示一个终结符号串的集合。
一个产生式集合，其中每个产生式包括一个称为产生式头或左部的非终结符号，一个箭头，和一个称为产生式体或右部的由终结符号及非终结符号组成的序列。主要用来表示某个构造的某种书写形式。
指定一个非终结符号为开始符号。

以只由数位和+，-符号组成的表达式为例，比如9-5+2、3-1或7。此文法的产生式包括：

list -> list + digit (2.1）
list -> list - digit (2.2)
list -> digit        (2.3)
digit-> 0|1|2|...|9  (2.4)

该文法的终结符号包括如下符号：

1	+ - 0 1 2 3 4 5 6 7 8 9

推导

根据文法推导符号串时，我们首先从开始符号出发，不断将某个非终结符号替换为该非终结符号的某个产生式的体。可以从开始符号推导得到的所有终结符号串的集合称为该文法定义的语言(language)。

由上面的文法定义的语言是由加减号分隔的数位列表的集合。

举例：推导出9-5+2是一个list。

1
2
3

因为9是digit，根据产生式（2.3）可知9是list。
因为5是digit，且9是list，由产生式（2.2）可知9-5也是list。
因为2是digit，9-5是list，由产生式（2.1）可知，9-5+2也是list。

在函数的参数列表中，函数参数可能为空串。在这种情况下，我们有如下文法：

$call \to id(optparams)\\opt \to params | \epsilon \\params \to params, params | param$

其中 $\epsilon$ 表示空串。

语法分析树

给定一个上下文无关文法，该文法的一颗语法分析树是具有以下性质的树：

根节点的标号为文法的开始符号。
每个叶子结点的标号为一个终结符号或空。
每个内部结点的标号为一个非终结符号。
如果非终结符号A是某个内部结点的标号，并且它的子结点的标号从左至右分别为 $X_1,X_2,...,X_n$ ,那么必然存在产生式 $A \to X_1X_2...X_n$

9-5+2的推导可以用下图来演示。

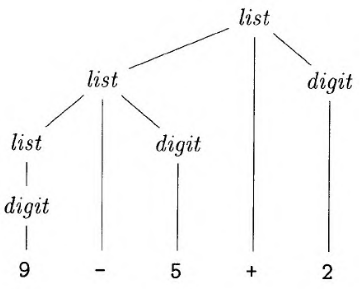
一颗语法分析树的叶子结点从左向右构成了树的结果，也就是从这颗语法分析树的根结点上的非终结符号推到得到的符号串。

一个文法的语言的另一个定义是指任何能够由某棵语法分析树生产的符号串的集合。

二义性

一个文法可能有多棵语法分析树能够生成同一个给定的终结符号串，这样的文法称为具有二义性。我们需要为编译应用设计出没有二义性的文法，或者在使用二义性文法时，使用附加的规则来消除二义性。

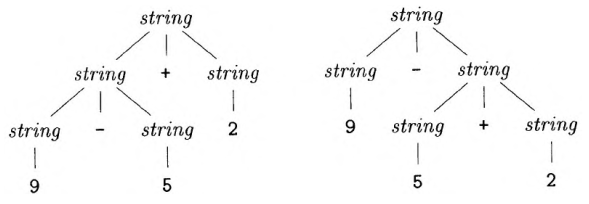
我们将list和digit都用string来表示，可以将上面的文法改写如下：

$string\to string+string | string - string | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9$

在使用这个文法时，9-5+2这样的表达式会有多棵语法分析树。

运算符的结合性

当一个运算分量的左右两侧都有运算符时，我们需要一些规则来决定哪个运算符被应用于该运算分量。我们说运算符+是左结合，因为当一个运算分量左右两侧都有‘+’号时，它属于其左边的运算符。常见的如加减乘除这四种元素符都是左结合的。

某些运算符是右结合的，比如赋值运算符‘=’。也就是说，表达式a=b=c等价于a=(b=c)。

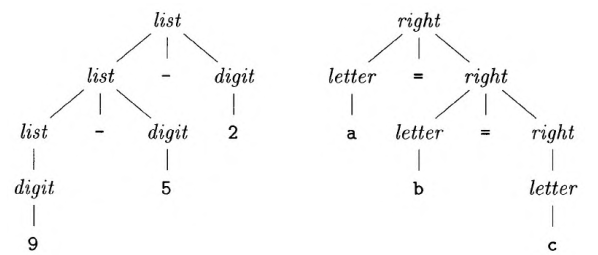
带有右结合运算符的串，比如a=b=c，可以由如下文法产生：

$right \to letter = right|letter\\letter\to a|b|...|z$

左结合与右结合的语法分析树。

运算符的优先级

对于表达式 $9+5*2$ ，有两种可能的解释，即 $(9+5)*2$ 或 $9+(5*2)$ 。因此，当多种运算符出现时，我们需要给出一些规则来定义运算符之间的相对优先关系。

算术表达式的文法可以根据表示运算符结合性和优先级的表格来构建。我们只考虑四个常用算术运算符和一个优先级表。同一行优先级相同，向下优先级递增。

1 2	左结合: +- 左结合: */

我们引入两个非终结符号expr和term，分别对应于这两个优先级层次，并使用另一个非终结符号factor来生产表达式中的基本单元。当前表达式的基本单元是数位和带括号的表达式。 $factor\to digit|(expr)$

然后考虑最高优先级的*和/， $term\to{term*factor\ |\ term/factor \ | \ factor}$

类似地，expr生成由加减运算符分隔的term列表： $expr \to{expr+term|expr - term| term}$

我们可以把上面的思想推广到具有任意n层优先级的情况。我们需要n+1个非终结符号，模仿这个例子。

练习

2.2.1

已完成，待上传

2.2.5

已完成，待上传